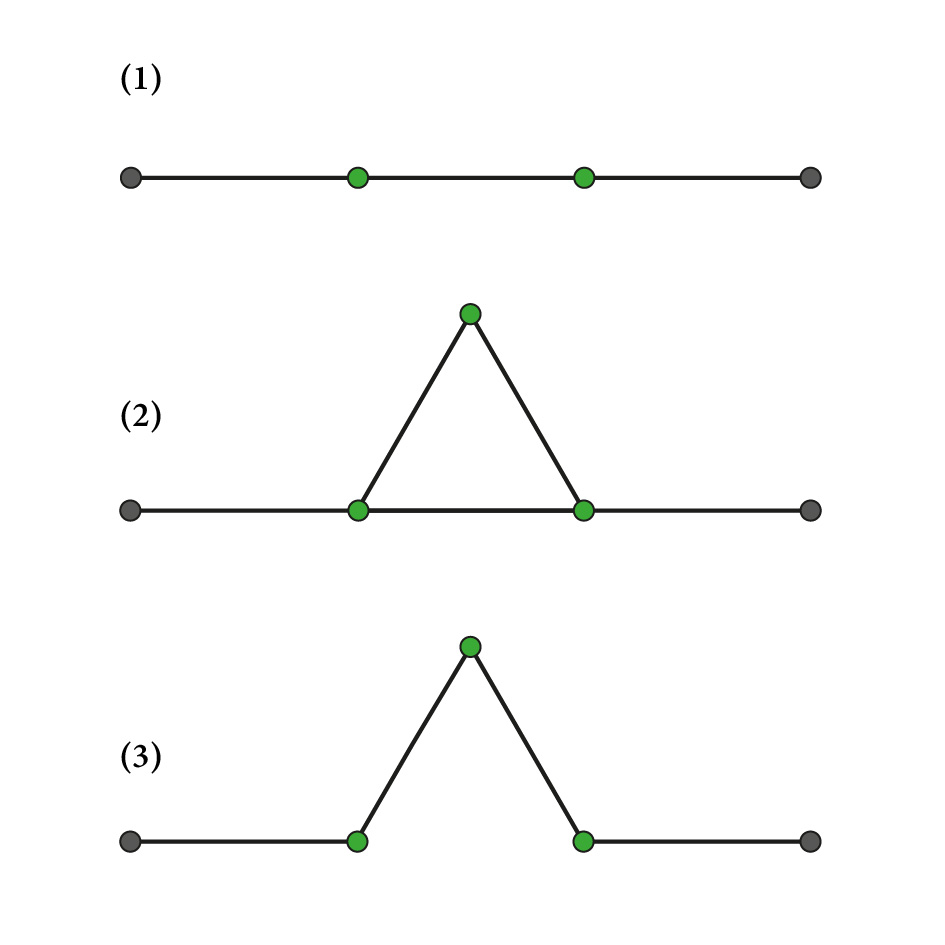
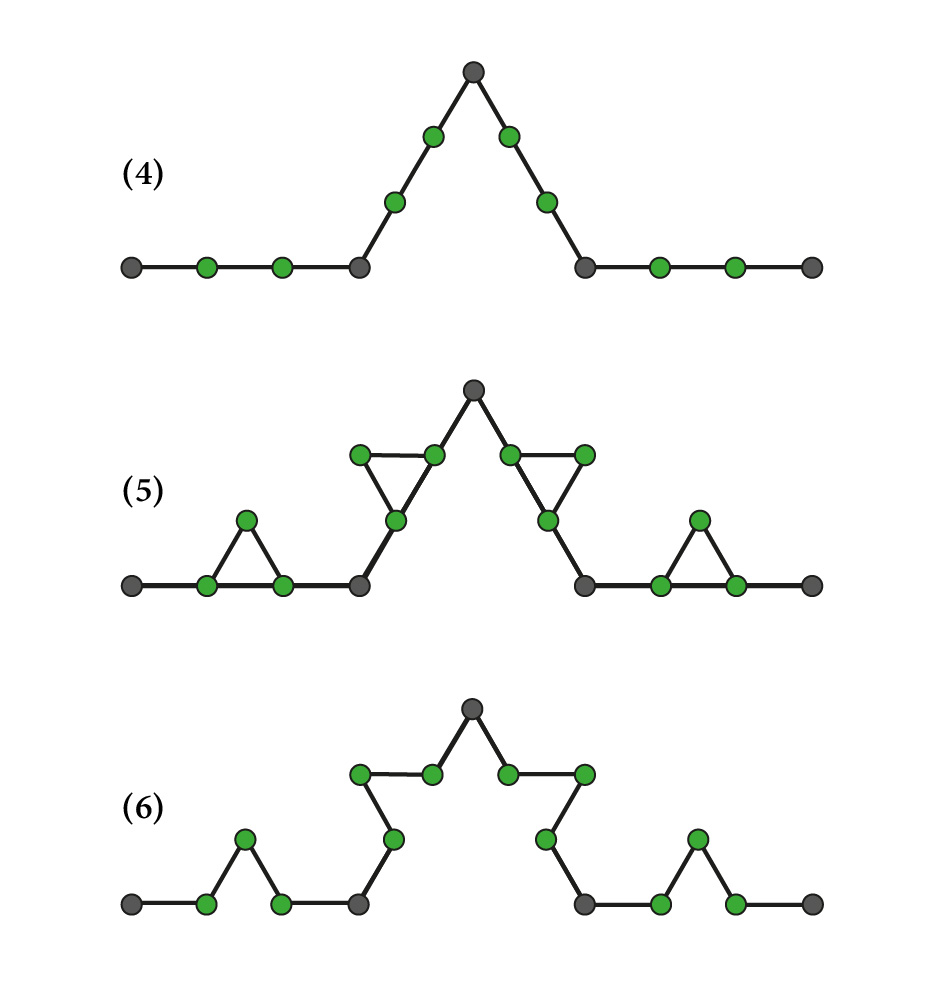
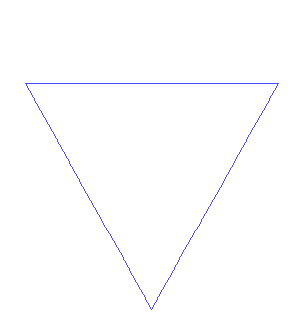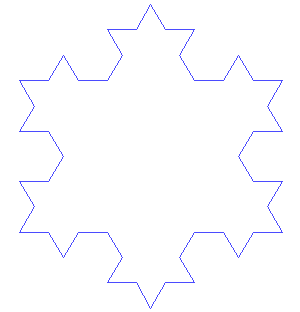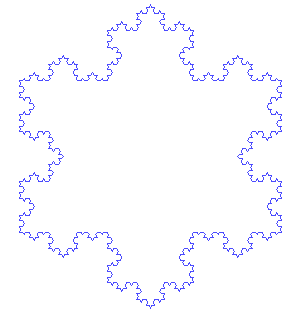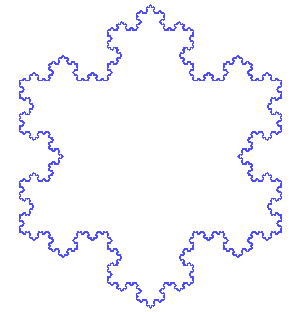
Les fractales sont des formes géométriques qui se répètent à différentes échelles. Cela signifie qu'une partie d'une fractale ressemble à l'ensemble de la fractale elle-même. C'est un peu comme si tu avais le dessin d'un arbre, puis que tu zoomais sur une branche de l'arbre et que cette branche ressemblait à l'arbre entier.
Le chou romanesco, fractale à déguster !
Le chou romanesco est un légume qui ressemble à une fleur. Il a une forme très particulière avec des branches qui se ramifient à partir d'un centre commun. Si tu regardes de plus près, tu peux voir que chaque petite branche a la même forme que la grande branche.