Fraktale sind geometrische Formen, deren Struktur sich in verschiedenen Massstäben wiederholt. Wenn du also einen Ausschnitt aus der fraktalen Form vergrösserst, ähnelt der vergrösserte Teil dem gesamten Fraktal. Am Beispiel des Tannenbaums kannst du dir vorstellen, dass du einen grossen Ast heranzoomst und dabei immer kleinere Zweige erkennst, die selbst wiederum verzweigt sind und in ihrer Struktur dem grossen Ast ähneln. Ein natürlich gewachsener Zweig verästelt sich vielleicht nur drei- oder viermal, doch in der Mathematik kann man solche Strukturen mit Formeln beschreiben und beliebig fortsetzen. Dabei entstehen geometrische Figuren, die schnell sehr komplex sind – und oft wunderschön aussehen.
Romanesco-Kohl: ein essbares Fraktal
Ein Fraktal aus der Natur: der Romanesco. Bild: Emilio Ereza - stock.adobe.com
Eines der schönsten Beispiele für ein natürliches, dreidimensionales Fraktal ist der Romanesco, eine spezielle Blumenkohl-Züchtung. Sein essbarer Blütenstand besteht aus zahllosen kegelartigen Strukturen, die an ihrer Oberfläche jeweils wieder Mini-Kegel tragen und so fort. Wenn du genauer hinschaust, erkennst du, dass jedes kleine Element in seiner Form dem gesamten Kohlkopf ähnelt.
Die Koch’sche Flocke – selbst konstruiert
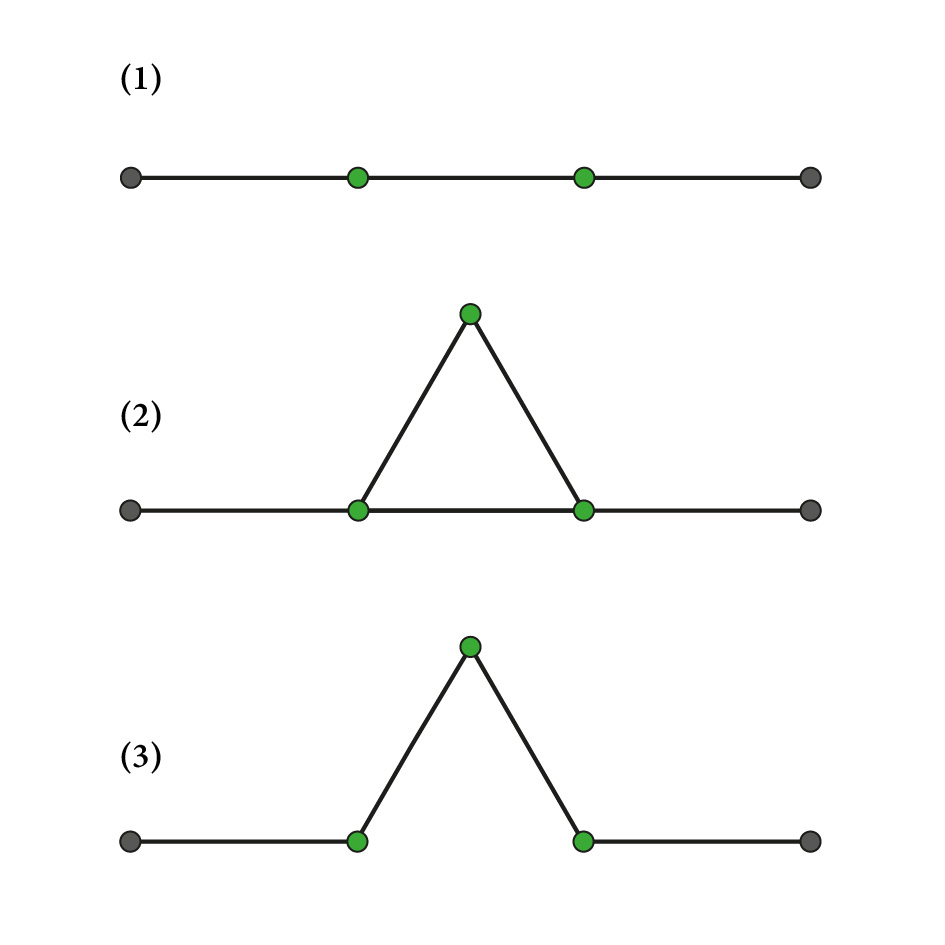
Konstruktion einer Koch’schen Kurve, Teil 1
Schneeflocken sind ein weiteres Beispiel für fraktale Formen, die in der Natur vorkommen. Eine mathematische Parallele dazu ist die Koch-Flocke, ein geometrisches Objekt mit der Form einer Schneeflocke. Sie wurde 1904 vom schwedischen Mathematiker Helge von Koch beschrieben, und du kannst sie Schritt für Schritt selbst zeichnen. Je grösser du anfängst (und je mehr Geduld du mitbringst), desto mehr Details wird deine Koch-Flocke bekommen.
Als erstes schauen wir uns die Konstruktion der Koch’schen Kurve an:
- Zeichne mit Bleistift eine Strecke. Teile die Strecke in drei gleich lange Abschnitte.
- Konstruiere ein gleichseitiges Dreieck über den mittleren Abschnitt (das heisst, der mittlere Abschnitt ist die Basis des Dreiecks).
- Radiere die Basis des Dreiecks aus.
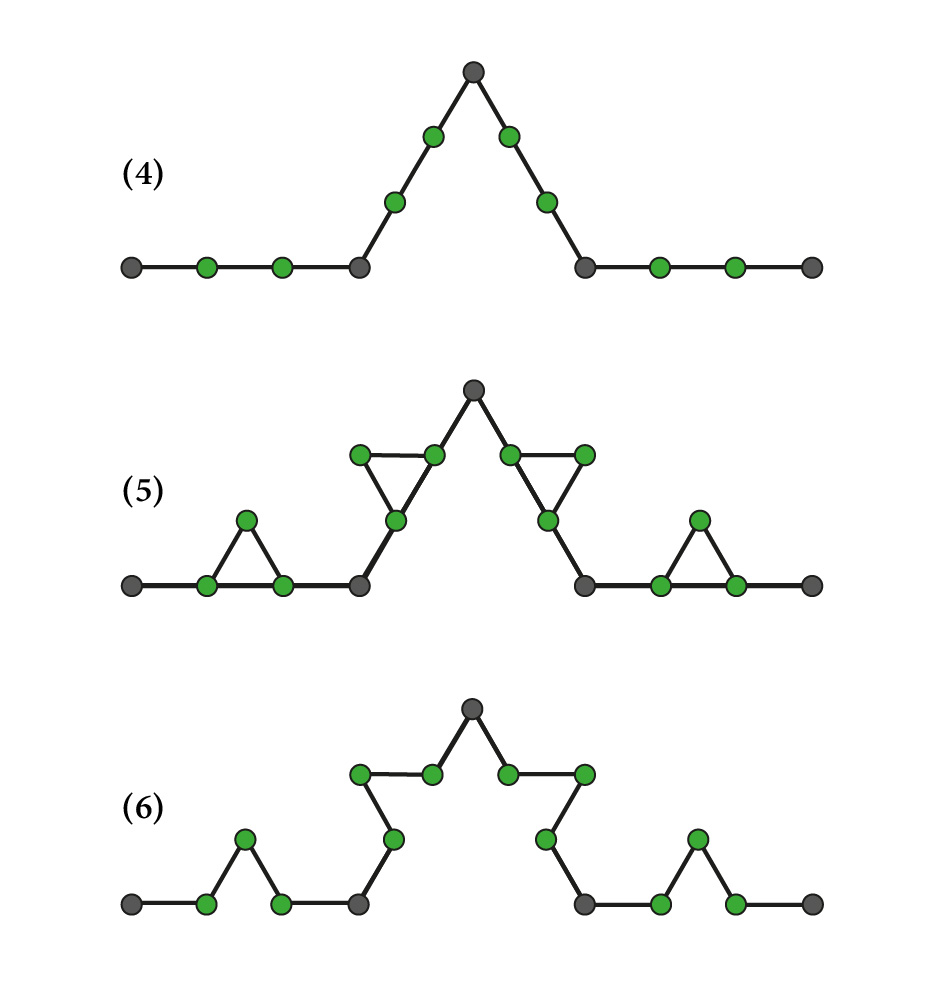
Konstruktion der Koch’schen Kurve, Teil 2
Die Form, die du nun vor dir siehst, besteht aus vier Abschnitten. Die Schritte 1.–3. werden nun für jeden der Abschnitte wiederholt:
- Teile jeden Abschnitt wiederum in drei gleich grosse Abschnitte.
- Konstruiere vier gleichseitige Dreiecke, eines in der Mitte jedes Abschnitts.
- Radiere die Basis der Dreiecke aus.
Die Koch’sche Flocke erhält man, wenn man statt von einer Strecke von einem gleichseitigen Dreieck ausgeht. Die oben beschriebene Methode wird auf jede Seite des Dreiecks angewendet und beliebig oft wiederholt – oder so lange, bis du nicht mehr kleiner zeichnen kannst … Du wirst eine Form mit zahlreichen, immer kleiner werdenden Spitzen und Spitzchen erhalten, und in jedem Ausschnitt kannst du einen Teil der Ursprungsform erkennen, mit der du begonnen hast. Eine Animation der Konstruktion einer Koch-Flocke siehst du weiter unten.
Mathematik in Bilder übersetzt
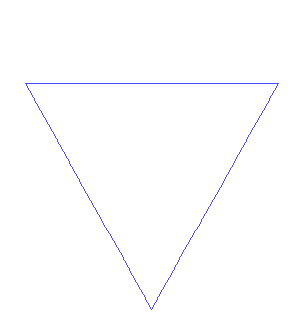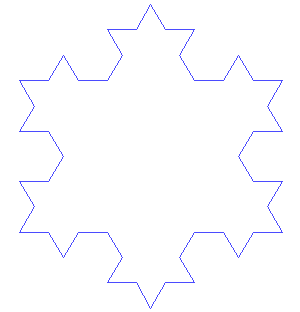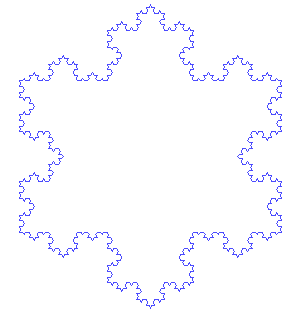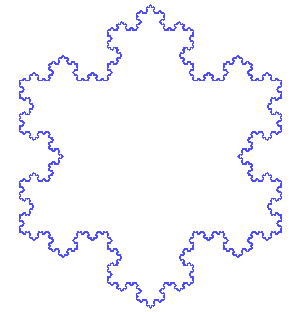
Konstruktion der Koch’schen Flocke. Bild: António Miguel de Campos/Wikimedia Commons
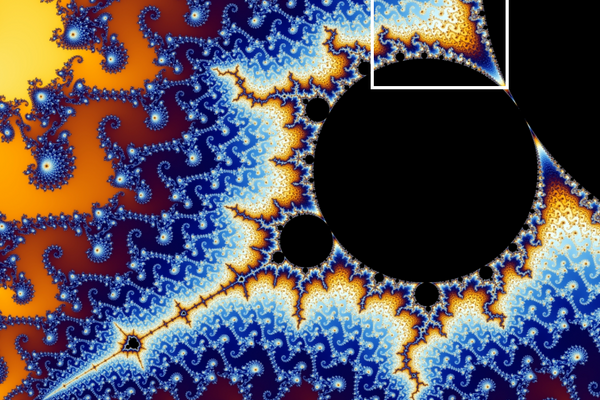
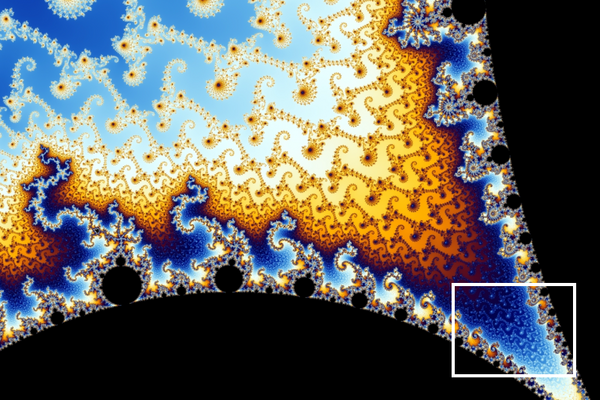
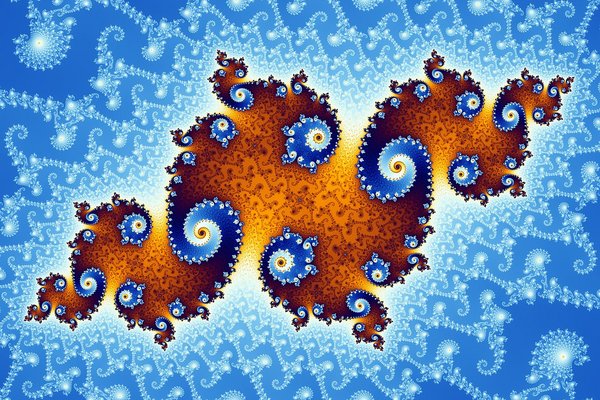
Die Koch’sche Kurve ist über hundert Jahre alt, der Begriff „Fraktal“ (vom lateinischen Wort für „gebrochen“) wurde aber erst 1975 von Benoît Mandelbrot geprägt. Nach diesem Mathematiker ist die sogenannte „Mandelbrot-Menge“ benannt, eine Teilmenge der komplexen Zahlen, die alle eine bestimmte mathematische Bedingung erfüllen (vereinfacht gesagt: man führt mit der Zahl eine bestimmte Rechenvorschrift durch; wenn das Ergebnis nicht unendlich ist, gehört die Zahl zur Mandelbrot-Menge). Am Computer kann man aus diesen Zahlen ein Bild generieren. Dazu ordnet man jedem Pixel eine Zahl zu, und entsprechend dem Ergebnis der Rechenvorschrift für diese Zahl erhält das Pixel eine bestimmte Farbe. So entsteht aus der Mandelbrot-Menge das unten gezeigte „Apfelmännchen“: ein Fraktal. Wenn man den Computer weiterrechnen lässt und die gezackten Ränder um den schwarzen Bereich heranzoomt, sieht man wunderschöne fraktale Strukturen und Muster, die zum Beispiel als Seepferdchen, Doppelspiralen, Kränze und Inseln bezeichnet werden. Dies kannst du in der untenstehenden Bildergalerie verfolgen.
Fraktale in Kunst und Wissenschaft
Computergenerierte Illustration in Form einer Blüte, basierend auf fraktaler Geometrie. Bild: Sebastian Baumer/Wikimedia Commons, CC BY-SA 3.0
Kein Wunder, dass sich fraktale Computerbilder auf der Basis von solchen Algorithmen zu einer eigenen Kunstrichtung entwickelt haben! Ein interessantes Beispiel ist der Bildschirmschoner „Electric Sheep“, der animierte und ineinander übergehende Fraktalbilder zeigt. Alle Computer, auf denen der Bildschirmschoner läuft, beteiligen sich an der Berechnung der Bilder. Dieser Prozess läuft im Hintergrund ab; die User greifen nur ein, um für besonders schöne Bilder abzustimmen und diese weiterentwickeln zu lassen.
Das Blatt eines Farns, ebenfalls ein Beispiel für eine fraktale Form aus der Natur. Bild: by-studio - stock.adobe.com
Auf der anderen Seite hat man fraktale Strukturen in immer mehr natürlichen Phänomenen entdeckt, zum Beispiel in Wolken und Wirbelstürmen, im Verlauf von Küstenlinien oder an der Oberfläche von Geweben wie Lunge oder Darm. Diese natürlichen Fraktal-Formen entstehen durch Zufallsprozesse und nicht durch eine exakte mathematische Vorschrift. Trotzdem sind sie, statistisch gesehen, den mathematischen Fraktalen so ähnlich, dass die Methoden der fraktalen Geometrie sich gut zu ihrer Beschreibung eignen. Ihre Eigenschaften können dadurch wissenschaftlich besser untersucht werden.